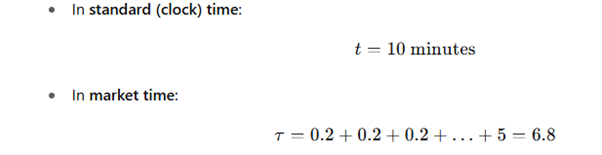我18岁的时候，曾和一些朋友一起去钓鱼。
在路上，汽车的一只轮胎爆胎了。车辆在路上翻滚了几次，最终掉进了沟里。
幸运的是，我们都没有受伤。
但事后回忆中，我们都记得事故发生的那一瞬间感觉异常漫长，即使对于外部观察者来说，一切只是几秒钟的事情。

这种现象经常由经历危急或威胁生命情况的人描述。
感觉就像时间本身变慢了。

我们习惯将时间视为一个线性维度，但根据狭义相对论，时间实际上是非线性的。

那么，如何将这种理解应用到外汇交易中？

外汇交易中的非线性时间

运动中的物体钟表相对于静止物体走得更慢（狭义相对论）

📘 科学解释：
如果一个物体以极高的速度运动（尤其是接近光速时），那么：

👉 物体运动得越快，相对于静止观察者而言，它的时间流逝得越慢。

⏰ 直观理解：
如果你身处一艘以光速99.999%速度飞行的宇宙飞船中，
你会感受到1小时的流逝，
而地球上则已过去10年。

换句话说，你在“穿越时间”。

📈 交易类比：

想象一下，一个市场中的价格以火箭般的速度急剧上涨。

• 在这一刻，市场时间被压缩 — 一切都在迅速发生。
• 对于参与其中的交易者而言，时间感觉是“正常”的。
• 而对外部观察者来说，它看起来像是突如其来的闪现。

🔵 强烈的市场冲击 = 相对论中的火箭。
🔵 移动中的时间相对于外部时间变慢。

靠近巨大物体时时间变慢

(🌌 广义相对论)

📘 科学解释：
引力本身不是一种“力”，而是质量导致的时空弯曲。
你距离一个巨大物体（如黑洞）越近，你的时间流逝就越慢。

⏰ 直观理解：

• 在地球轨道上，时间比地面上流逝得更快。
• 靠近黑洞时，时间几乎停止。

对外部观察者来说，物体似乎在事件视界“冻结”了，但其内部时间依旧正常流动。

📈 交易类比：
巨大的引力体 = 重大市场事件（例如NFP报告、FOMC会议、地缘政治冲击）。

当市场接近此类事件时：

• 价格行动放缓（因为预期），
• 成交量收缩（交易者观望），
• 市场时间被拉长，仿佛现实被“暂停”。

而在事件之后 — 市场时间“爆发”，价格剧烈波动。

🧠 总结表格 — 物理 vs 交易：

物理概念	交易类比
🚀 高速运动	市场冲击、突破、新闻事件
⌛ 时间膨胀（变慢）	横盘、筹码堆积、等待新闻
🌌 引力	主要参与者或基本面因素的影响
📉 时间扭曲	ATR扩张、波动爆发、非线性市场时间

 

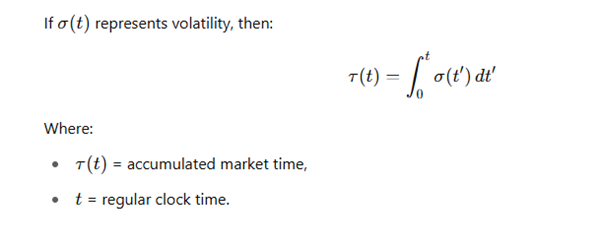
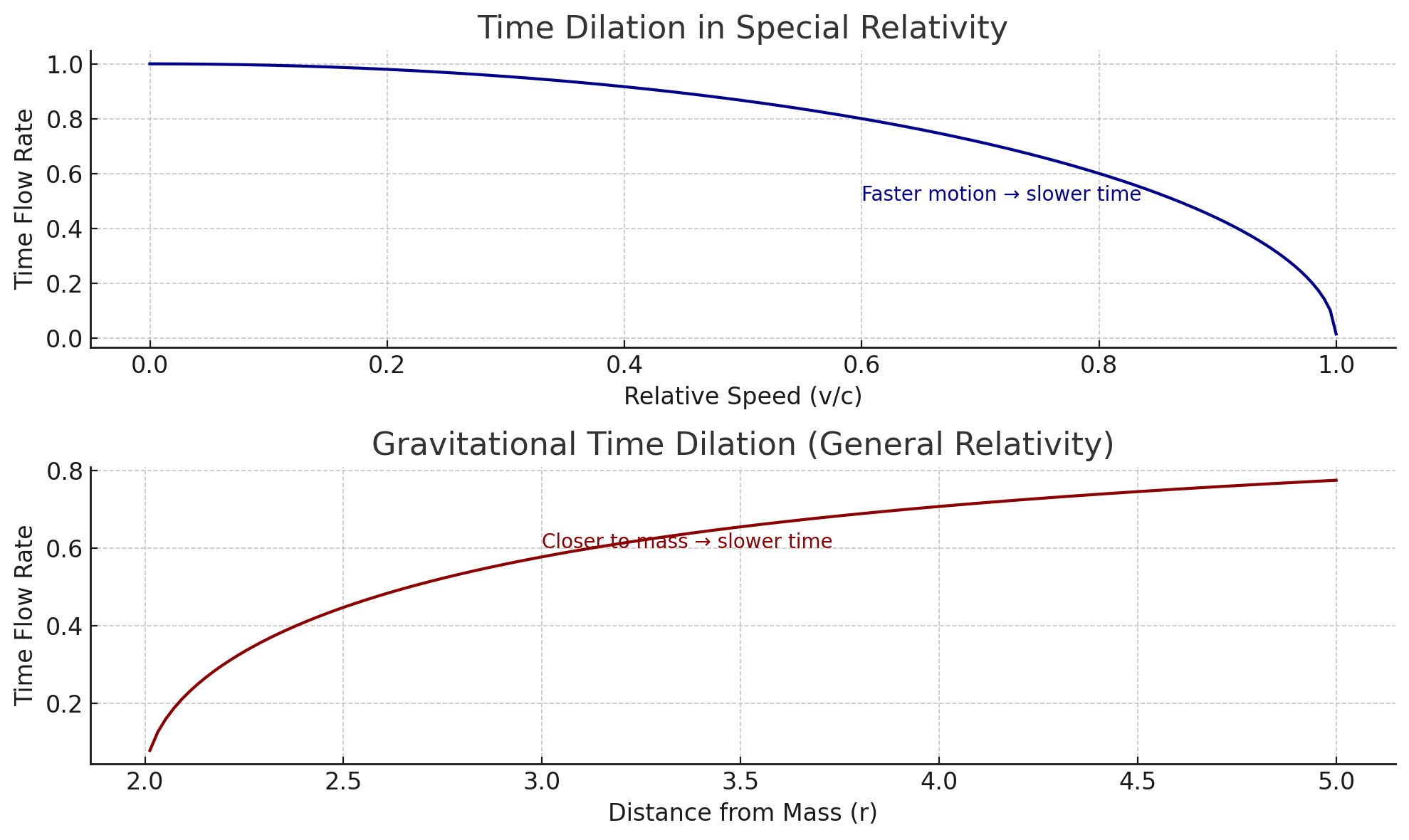
以下是时间在物理学中的非线性行为的视觉解释，以及它如何与交易相关联：

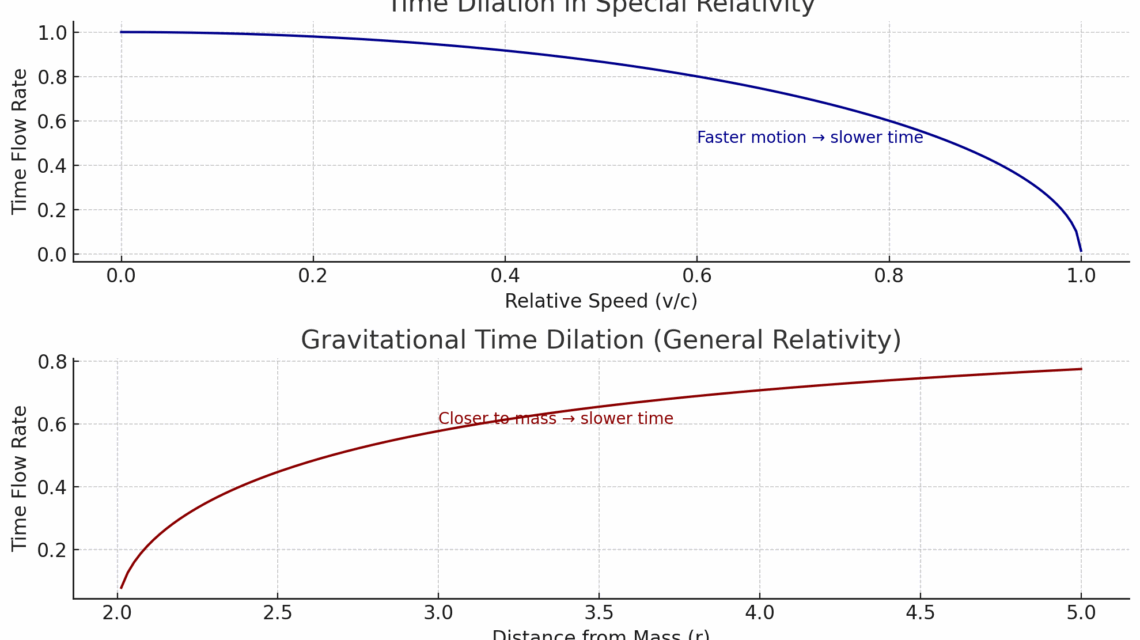
🔷 图表 1：狭义相对论 — 速度使时间变慢

• 物体运动得越快（越接近光速），相对于静止观察者来说，时间流逝越慢。
• 交易中：
  📈 高速市场运动（冲击）对内部参与者来说压缩时间 — 一切感觉快速但平滑。

🔴 图表 2：广义相对论 — 引力使时间变慢

• 物体距离引力质量越近，由于时空弯曲，时间流逝越慢。
• 交易中：
  🧲 重大经济事件（NFP、FOMC、地缘风险）就像引力井一样。
  市场变慢、冻结、积压压力 — 时间延展、波动压缩。

💡 外汇交易中非线性时间的示例

想象一张EUR/USD的10分钟走势图：

• 前9分钟市场横盘（价格波动仅在3个点以内），
• 第10分钟由于新闻导致波动剧增，价格跳涨30点。

⏰ 在线性时间中：

• 所有10分钟被视为同等重要。
• 如SMA、RSI、MACD等指标只做平均处理，不区分实际影响。

🌀 在“市场时间”（非线性时间）中：

• 9分钟的横盘被压缩 — 几乎没有长度。
• 那1分钟的高波动被扩展 — 在“市场时间”中相当于整天。
• 指标在横盘期变慢，在活动爆发时加快。

📊 物理类比：

狭义相对论：

• 高速运动中的钟表走得比静止观察者慢。

广义相对论：

• 在巨大质量体附近，时间会被拉长（引力时间膨胀）。

交易中：

• 横盘市场像静止物体 → 时间几乎静止。
• 价格冲击像跳跃到超空间 → 时间飞逝。

🔍 市场时间公式：

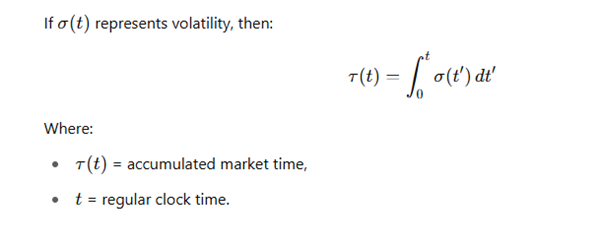
📏 数值示例：

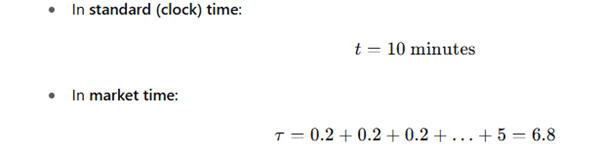
这1分钟的波动性远远大于那9分钟的沉寂。

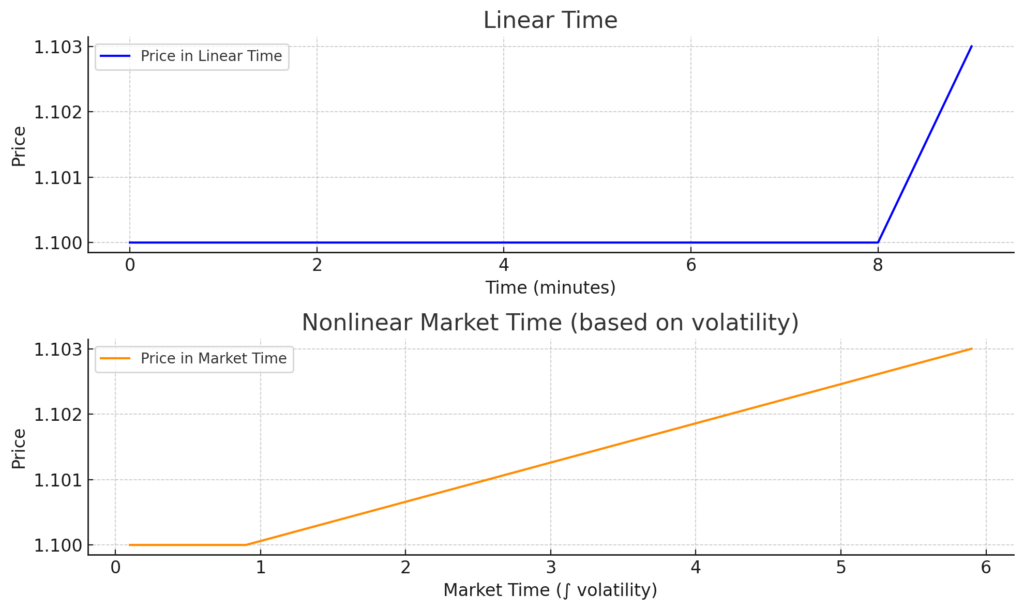
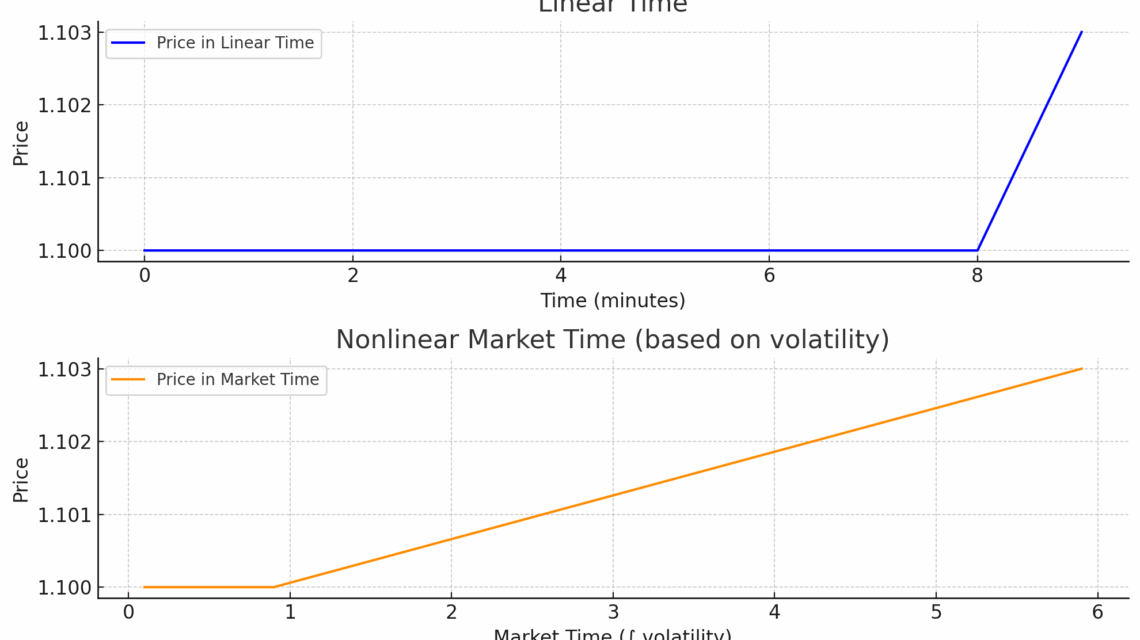
以下是交易中非线性时间的可视化演示：

🔷 顶部图表：线性时间

• 每一分钟都被平等对待。
• 价格在9分钟内平稳，最后一分钟突然跳升。

🟠 底部图表：非线性市场时间

• 时间基于波动性（市场活动）被拉伸。
• 最后那一分钟高波动被“扩展”，而平稳时段被压缩。
• 这模拟了相对论时间：更多运动 = 更多“体验时间”。

🧠 实际操作中，基于市场时间构建的指标：

• 对重要变化做出更快速响应。
• 忽略信息含量低的横盘区域。
• 更贴近交易者在高波动时刻对时间的“主观感受”。

🔍 外汇标准技术指标的问题

如RSI、MACD、移动平均等指标：

• 假设时间是线性且绝对的，
• 在固定刻度上运行（第1根K线、第2根K线…），
• 无法适应市场的“压缩”或“膨胀”。

📌 现实中，市场运行在非线性时间下：

• 有时，5分钟的重量等同于1小时（高波动），
• 而有时，3天如影而过（低波动，横盘）。

🚀 如果我们采用相对论方法呢？

🔸 理念：将市场视为一个时空结构，其中：

• 价格 = 坐标xxx，
• 时间 = ttt，
• 但时间并非绝对 —— 它是市场相对的。
• 图表上的每一个点 = 时空中的事件。

🔬 我们可以构建什么样的外汇技术指标？

🔧 相对论 RSI（RRSI）：

• 一个普通的RSI，但基于非线性时间尺度计算。
• K线按“加速时间”τ(t)加权。
• 波动性剧烈时，时间被拉伸 —— RSI反应更迅速。

🤯 或者：

🧭 时间曲率指数（TCI）：

• 衡量市场时间的弯曲程度及方向：
  • 📈 正曲率 → 加速（如引力吸引），
  • 📉 负曲率 → 减速或停滞。

⚙️ 实施思路：

• 用市场时间加权ω代替普通K线重新计算指标。
• 将其可视化为一个扭曲的网格，如广义相对论中的时空图。
• 使用机器学习对市场度量建模（波动率、成交量、tick密度、新闻反应等）。

🚀 附加：如何在实践中计算波动率积分

📘 在相对论中：

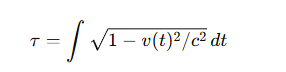
📈 在市场中：

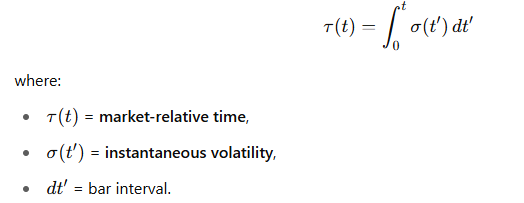
🛠 如何实际计算：

🔸 步骤1：估算波动率 σ(t)

方法选项：

💠 绝对波动：

sigma = abs(price[t] - price[t-1])

💠 滑动标准差：

sigma = price_series.rolling(window).std()

💠 ATR（平均真实波幅）：

import ta
sigma = ta.volatility.AverageTrueRange(high, low, close, window=14).average_true_range()

🔸 步骤2：对波动率进行积分

对于离散数据，使用简单的累计和：

rel_time = np.cumsum(sigma.values)

于是，rel_time[i] 表示市场在其“内部时间”中“走过了多远”。

---

📊 简单 Python 示例：

import numpy as np
import pandas as pd

# 假设有一个价格数组
price = np.array([...])

# 计算绝对波动
sigma = np.abs(np.diff(price, prepend=price[0]))

# 积分波动性
rel_time = np.cumsum(sigma)

>>>Learn more about professional software for Arbitrage Trading – SharpTrader